Farm finance and liquidity
Introduction
The basic idea is that investment require liquidity, and liquidity can be obtained using open-credit line that can grow up to a model-fixed share of the capital (e.g. 80%).
Each year the farmer optimize the quantity of money to ask from the bank. There isn't a end-term to give back the money. The limit is as share of the capital.
Differently from the original AgriPoliS there is no difference from shot-term loans and long-terms one. This is because loans are completely decoupled from investments. On the other side, there is no need to assume a constant share of investment covered by the loan: the individual farmers are free to implicitly optimize the share of the investments covered by loans depending on their financial situation.
Matrix
This would be a typical matrix involving investments, with activities on columns and resources on rows:
| Resources | Prod. activity 1 | Prod. activity 2 | Animal act1 | Inv. activity 3 | Stables large | Stables small | Buy liquidity | Sell liquidity | Used resourses | Available resources | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gross margin | 60 | 300 | 500 | 280 | -5000 | -2500 | -0.04 | 0.03 | ||||
| Liquidity | 20 | 20 | 50 | 5000 | 100000 | 50000 | -1 | 1 | 0 | -2000 | ||
| Debs level | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 6000 | ||
| PlotX | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 6000 | ||
| Stables animal1 | 0 | 0 | 1 | 0 | 30 | 8 | 0 | 0 | … | … | ||
| … | … | … | ||||||||||
| Oth. spec. resources | … | … | … | … | 0 | 0 | 0 | 0 | … | … | ||
| … | ||||||||||||
| Quantity | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Formula
Liquidity is calculated as follow:
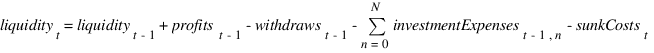
with 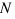 mumber of investments made on the previous year. Activity products require a limited level of liquidity as imprest fund while investments get the whole initial cost as liquidity requirement.
mumber of investments made on the previous year. Activity products require a limited level of liquidity as imprest fund while investments get the whole initial cost as liquidity requirement.
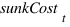 are made by the cost of rented plots and eventually (not in the model now) by investment maintenance costs.
are made by the cost of rented plots and eventually (not in the model now) by investment maintenance costs.
The available deb level is the X% of the whole capital, calculated as:
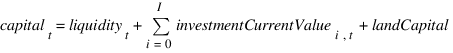
with 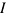 is the number of owned investment on current year. The current value of investment objects depend from the kind of investment itself: e.g. in perennial crops the value first grow up and then decrease, in stables it linearly decrease, and so on..
is the number of owned investment on current year. The current value of investment objects depend from the kind of investment itself: e.g. in perennial crops the value first grow up and then decrease, in stables it linearly decrease, and so on..
The  is, at least for now, fixed and read from file at init stage.
is, at least for now, fixed and read from file at init stage.
The capital, as well the deb level, do not exists as proprieties, but is dynamically calculated with the function getCapital().
Investments
Investments are always modeled as integer. However they differ on two aspects:
- Explicit or implicit link with the associated activity(es).
If investments are not offered in different size classes and are needed for the production of only one product, they can be modeled as a individual activity composed of the investment and the associated activity product.
In this case the gross margin is equal to the average product gross margin minus the average investment costs, the liquidity is equal to the investment initial cost plus the imprest fund and all the other specific requirements needed by the activity apply.
The other alternative (not applicable if the object are space explicit) is to provide two or more separate options of the investments and the activity. In this latter case the gross margin is equal to minus the average yearly cost, but the investment provide a resorse
(e.g. stables) needed by the activity. Decoupling the investment from the activity we can model scale effects.
- Spacial explicitness.
If the object is spacial explicit (associated with one specific plot) one investment option is to be gived for each plot suitable to guest it (compatible land type). This allow us to consider the shadow price not only of the liquidity capital but also of the land. Following years (up to the time length of investment for activity 3) plotX will be fixed to activity 2 and it will not be available, eg. for activity 2.
Investment ownership
Fixed investment (without space attributes) are owned by agents (and are directly in their “portfolio”, in the program terms are in their myObjects vector).
For spatial objects the question is little more complicated.
If a plot is rented, you can have already spatial objects on them or you can rent the plot and add to it the spatial object (typically, plants).
So, rather than being in the agent portfolio, spatial objects are kept in the plot portfolio. However objects kept track of their owner thanks to pointers. So if the plot is rented we label the new object to be owned by the plot tenant, otherwise we label the object to be owned by the plot owner.